Suiv.: Cas axisymétrique Sup.: 2 Thermique bidimensionnelle Préc.: 2.2 Formulation variationnelle Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: Cas axisymétrique
Sup.: 2 Thermique bidimensionnelle
Préc.: 2.2 Formulation variationnelle
Index
Table des matières
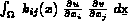 ,
,
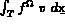 ...
Dans tout ce qui suit, on considère le cas d'une formulation en
température, sans tenir compte des effets des déformations d'origine élastique initiales.
...
Dans tout ce qui suit, on considère le cas d'une formulation en
température, sans tenir compte des effets des déformations d'origine élastique initiales.
Le passage aux quantités élémentaires est identique au cas de la dimension 3.
Soient 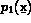 ,
, 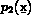 , ...,
, ..., 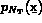 les
les 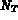 fonctions de base. On note
fonctions de base. On note
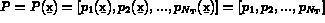
Alors,
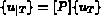
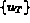 la restriction à T de { u }, valeurs
de la fonction u aux noeuds de l'élément T.
la restriction à T de { u }, valeurs
de la fonction u aux noeuds de l'élément T. Ensuite, on note
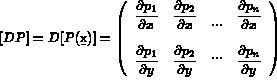
De même, on exprime  en fonction de
[ D P] et de
en fonction de
[ D P] et de  par
Par définition même de la méthode, on a:
par
Par définition même de la méthode, on a:
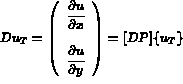
Avec pour matrice de conductivité (sous sa forme générale) :
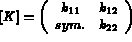
on peut calculer sur chaque élément T:
 la matrice élémentaire de masse,
la matrice élémentaire de masse,
 la matrice élémentaire de rigidité,
la matrice élémentaire de rigidité,
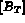 le second membre élémentaire et
le second membre élémentaire et
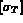 les flux élémentaires
les flux élémentaires
Pour obtenir le système à résoudre, il suffit de construire les matrices et seconds membres globaux (voir également le cas de la dimension 3 paragraphesec:sysglob3ther).