Modulef
Next: 7.7 Sorting and dichotomy Up: 7 Internal programs Prev: 7.5 Conversions Contents

7.6 Matrix and vector manipulations

      SUBROUTINE NRMVCT(V1, V)
      REAL V1(3), V(3)

Normalization of vector V1:

      SUBROUTINE PRDVCT(V1, V2, V)
      REAL V1(3), V2(3), V(3)

Vector product : V=V1*V2

       REAL FUNCTION PRDSCL(V1, V2)
       REAL V1(3), V2(3)

Scalar product : PRDSCL=V1.V2

      REAL FUNCTION PRDMXT(V1, V2, V3) 
      REAL V1(3), V2(3), V3(3)
      EXTERNAL PRDSCL
      REAL PRDSCL

Mixed product : PRDMXT=V1.(V2*V3)

```
      SUBROUTINE  NORMAL(CC)
      REAL CC(4)
```
converts CC(1:4), in homogeneous coordinates, into normal coordinates. (i.e. such that CC(4) = 1.).

Calling subroutines which perform transformations in the three-dimensional space, initiates matrix computations corresponding to the linear application associated with the transformation.

Other subroutines perform clipping computations (see masks and windows). Generally, the user does not deal with these subroutines. However, for certain computations (not necessarily graphical!), it is possible to employ these subroutines of practical interest, advantageously.

It is however necessary to stress certain notions.

The internal procedures in FORTRAN 3D manipulate a real type 4*4 matrix, henceforth called MAT(4, 4), consisting of a 3*3 sub-matrix, representing the rotation, and a vector corresponding to the last column, representing the translation. The lower right-hand corner of this matrix contains a 1. and the three first elements in the last line are zero, as shown below:

 
    MAT(1:3, 1:3)   ---> Rotation                |  R  R  R  T  |
    MAT(1:3,  4 )   ---> Translation             |  R  R  R  T  |
                                                 |  R  R  R  T  |
    MAT(4, 1:4)     --->                         |  0  0  0  1. |

Before performing any matrix operations, MAT must be initialized to a unit matrix. The transformation procedures are then called sequentially, each multiplying the matrix with a matrix corresponding to the transformation. At the end of the operations, the matrix contains the result of all the operations performed.

```
      SUBROUTINE MATUNI(MAT)
      REAL MAT(4, 4)
```
returns a unit matrix in MAT . The call to this procedure is obligatory before using the subroutines mentioned below.
```
      SUBROUTINE LDMAT(MAT)
      REAL MAT(4, 4)
```
returns the matrix at the current stack level in MAT . This procedure can replace the preceding one if we wish to perform transformations relative to the current level of operations in progress, instead of starting with the identity matrix.

      SUBROUTINE PRDMAT(MAT1, MAT)
      REAL MAT1, MAT

returns the matrix product : MAT = MAT1 * MAT in MAT.

```
      SUBROUTINE TRSFO1(P, MAT)
      REAL P(4), MAT(4, 4)
```
returns the product : P = P*MAT in vector P. After transformation, P is in homogeneous coordinates.
```
      SUBROUTINE INVMAT(MAT, MAT1)
      REAL MAT(4, 4), MAT1(4, 4)
```
returns the inverse of MAT , calculated by the Gauss-Jordan method (maximum pivot) in MAT1.
```
      SUBROUTINE TRSLL(A, B, C, MAT)
      REAL A, B, C, MAT(4, 4)
```
The translation is defined by: X = X + A , Y = Y + B et Z = Z + C . Calculate a translational matrix, M1, and then store the matrix product, MAT = M1 * MAT , in MAT.
```
      SUBROUTINE ROTT(I, BETA, MAT)
      INTEGER I
      REAL BETA, MAT(4, 4)
```
calculates a rotational matrix , M1, of an angle BETA around an axis defined by the value in I: I=1 axis 0X, I=2 axis 0Y, or I=3 axis 0Z, and then returns the matrix product, MAT = M1 * MAT , in MAT.
```
      SUBROUTINE SCALEE(A, B, C, MAT)
      REAL A, B, C, MAT(4, 4)
```
Scale : X = A * X , Y = B * Y et Z = C * Z. Calculate a scaling matrix, M1, perform the matrix product, MAT = M1 * MAT, and return the result in MAT.
```
      SUBROUTINE SHEARR(A, B, C, MAT)
      REAL A, B, C, MAT(4, 4)
```
Define a shearing matrix, i.e. the following transformation:

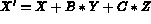
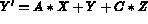
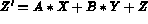
Then return the matrix product, MAT = M1 * MAT, in MAT.
```
      SUBROUTINE REPERR(XO, YO, ZO, XR, YR, ZR, IVERTI, MAT)
      REAL XO, YO, ZO, XR, YR, ZR, MAT(4, 4)
      INTEGER IVERTI
```
where:
(XO, YO, ZO): the position of the observer in the object's coordinate system;
(XR, YR, ZR): represents the coordinates of the point viewed in the same coordinate system;
IVERTI: the vertical of the initial coordinate system:
IVERTI = 1 OX vertical
IVERTI = 2 OY vertical
IVERTI = 3 OZ vertical

We can thus associate a local coordinate system with the observer such that he is positioned at the origin, looking in the negative Z direction (normalized position).
This subroutine calculates this transformation's matrix, M1, and then returns the matrix product, MAT = M1 * MAT, in MAT.
See also subroutine NRMLST.
```
      SUBROUTINE ROTAXX(PX, PY, PZ, VX, VY, VZ, THETA, MAT)
      REAL PX, PY, PZ, VX, VY, VZ, THETA, MAT(4, 4)
```
calculates a rotational matrix , of an angle THETA radians around the axis defined by the origin vector, (PX, PY, PZ), and component vector, (VX, VY, VZ), and then returns the matrix product, MAT = M1 * MAT, in MAT.
This corresponds to subroutine ROTAXE.
```
      SUBROUTINE SYMTRR(I, J, MAT)
      REAL MAT(4, 4)
      INTEGER I, J
```
This subroutine calculates a symmetry matrix, M1, and then returns the matrix product, MAT = M1 * MAT, in MAT, where:
I=1: symmetry w.r.t. the origin;
I=2: symmetry w.r.t. a plane: J=1: x0y, J=2: y0z, J=3: z0x;
I=3: symmetry w.r.t. an axis: J=1: 0x, J=2: 0y, J=3 0z.

See subroutine SYMTRI.
```
      SUBROUTINE POS3DD(P1, P2, P3, Q1, Q2, Q3, MAT)
      REAL P1(3), P2(3), P3(3), Q1(3), Q2(3), Q3(3), MAT(4, 4)
```
calculates a transformation matrix, M1, and returns the matrix product, 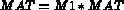, in MAT. The matrix, MAT, positions the object defined by P1, P2, P3 at Q1, Q2, Q3.
See subroutine POS3D.

Next: 7.7 Sorting and dichotomy Up: 7 Internal programs Prev: 7.5 Conversions Contents