Suiv.: tetrip1d Sup.: 9 Fiches techniques Préc.: tria2p1v Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: tetrip1d
Sup.: 9 Fiches techniques
Préc.: tria2p1v
Index
Table des matières
DESCRIPTION DE L'ELEMENT
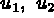 les composantes tangentielles,
les composantes tangentielles, 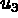 la
composante normale,
la
composante normale, 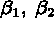 les composantes de la rotation
de la normale
les composantes de la rotation
de la normale
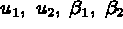
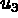
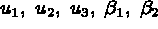
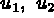
Coordonnées sur l'élément de référence:
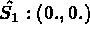
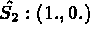
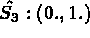
INTEGRATION NUMERIQUE
Consultez le Rapport de Recherche INRIA 699
LES DONNEES A FOURNIR (en double précision)
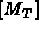 , partie
, partie 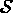
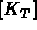 , partie
, partie 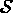
 supposés constants par élément
supposés constants par élément
Le paramètre NOTEL permet de spécifier le type d'intégration à utiliser
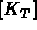 si il est
calculé, rien sinon (les contraintes sont calculées aux 3 noe uds sommets)
si il est
calculé, rien sinon (les contraintes sont calculées aux 3 noe uds sommets)
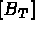 , partie
, partie 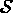
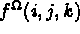 pour i=1,NDSM; j=1,6; k=1,npis;
pour i=1,NDSM; j=1,6; k=1,npis;
SOUS-PROGRAMME UTILISATEUR A FOURNIR
Pour définir la surface moyenne de la coque, on doit écrire le s.p suivant:
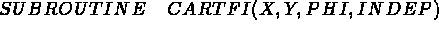
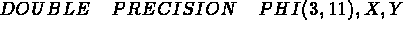
C les 3 composantes de PHI :
PHI(J,1) = ... pour J=1,3
C les 3 composantes de 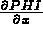 :
PHI(J,2) = ... pour J=1,3
:
PHI(J,2) = ... pour J=1,3
C les 3 composantes de 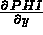 :
PHI(J,3) = ... pour J=1,3
:
PHI(J,3) = ... pour J=1,3
C les 3 composantes de 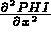 :
PHI(J,4) = ... pour J=1,3
:
PHI(J,4) = ... pour J=1,3
C les 3 composantes de 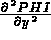 :
PHI(J,5) = ... pour J=1,3
:
PHI(J,5) = ... pour J=1,3
C les 3 composantes de 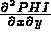 :
PHI(J,6) = ... pour J=1,3
:
PHI(J,6) = ... pour J=1,3
C les 3 composantes de 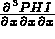 :
PHI(J,7) = ... pour J=1,3
:
PHI(J,7) = ... pour J=1,3
C les 3 composantes de 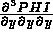 :
PHI(J,8) = ... pour J=1,3
:
PHI(J,8) = ... pour J=1,3
C les 3 composantes de 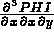 :
PHI(J,9) = ... pour J=1,3
:
PHI(J,9) = ... pour J=1,3
C les 3 composantes de 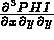 :
PHI(J,10) = ... pour J=1,3
:
PHI(J,10) = ... pour J=1,3
C l'épaisseur et ses 2 dérivées 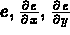 :
PHI(J,11) = ... pour J=1,3
:
PHI(J,11) = ... pour J=1,3
END