Suiv.: 2.2 Formulation variationnelle Sup.: Elasticité bidimensionnelle Préc.: Elasticité bidimensionnelle Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: 2.2 Formulation variationnelle
Sup.: Elasticité bidimensionnelle
Préc.: Elasticité bidimensionnelle
Index
Table des matières
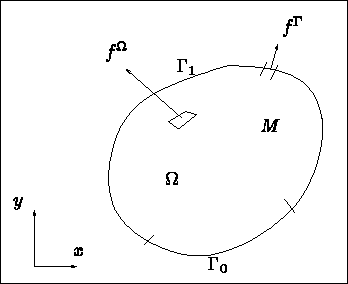
Figure: Présentation du problème
La modélisation en E.D.P. s'écrit comme:
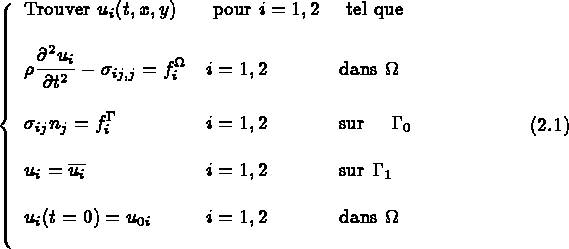
avec
 la densité du matériau,
la densité du matériau,
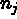 la composante j de la normale unitaire extérieure à
la composante j de la normale unitaire extérieure à 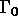 ,
,
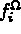 les efforts surfaciques appliqués à
les efforts surfaciques appliqués à
 et
et 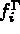 les efforts linéiques appliqués sur
les efforts linéiques appliqués sur 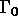 ,
,
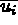 le déplacement imposé sur
le déplacement imposé sur 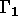 ,
,
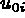 la condition initiale (t=0),
item
la condition initiale (t=0),
item 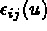 le tenseur des déformations linéarisé
symétrique de Green Lagrange (hypothèses des petites déformations)
le tenseur des déformations linéarisé
symétrique de Green Lagrange (hypothèses des petites déformations)
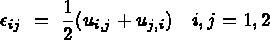
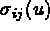 le tenseur des contraintes
le tenseur des contraintes
où 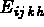 désigne le tenseur d'élasticité.
Ce tenseur vérifie les propriétés suivantes :
désigne le tenseur d'élasticité.
Ce tenseur vérifie les propriétés suivantes :
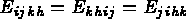
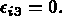 ),
lorsque le milieu continu est homogène isotrope,
la loi de comportement (loi de Hooke) s'écrit
en fonction des coefficients de Lamé
),
lorsque le milieu continu est homogène isotrope,
la loi de comportement (loi de Hooke) s'écrit
en fonction des coefficients de Lamé 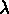 et
et 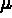 :
:

où 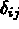 est le symbole de Kronecker.
est le symbole de Kronecker.
Les coefficients de Lamé 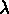 et
et 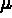 sont reliés à E le module de Young et
sont reliés à E le module de Young et  le
coefficient de Poisson (cf 1.4)
le
coefficient de Poisson (cf 1.4)
De plus,
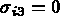 .
Ceci implique que
.
Ceci implique que 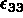 est non nul et s'exprime en fonction de
est non nul et s'exprime en fonction de 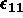 et
et 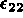 .
En particulier, dans le cas d'un matériau homogène isotrope, la loi de
comportement devient :
.
En particulier, dans le cas d'un matériau homogène isotrope, la loi de
comportement devient :
en posant 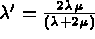 ,
2.4 s'écrit :
,
2.4 s'écrit :

Cette forme étant analogue à la précédente, le même traitement permet de résoudre les 2 problèmes.